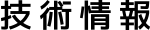基礎シリーズ第5弾。てこの原理で地球も動かせる?倍力機構の概要&てこ、トグル、クランク機構を用いた使用事例をご紹介
- 倍力機構とは / てこ機構
- トグル機構
- 倍力機構の使用例
倍力機構の使用例① てこを使った簡易プレス機
簡易プレス機
図5 簡易プレス機のメカニズム
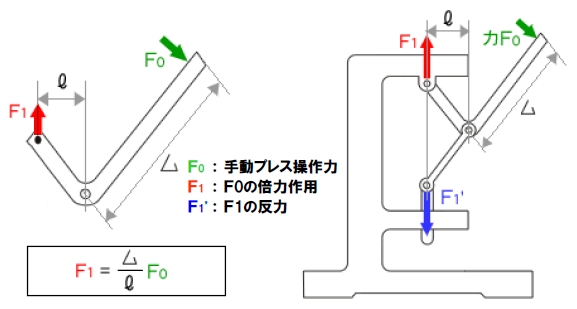
図5の機構は、ベルクランクとトグルジョイントクランクを組み合わせた簡易プレス機です。
ベルクランクのハンドル部に加えてた力(F0)が、倍力メカニズムで腕の長さ比に応じて倍力(F1)が得られ、
その力をプレス機の筐体で支え、その反力をトグルジョイントで反対方向に変向し、プレス加工力(F1’)とする機構です。
倍力機構の応用例② クランク・トグル機構を使ったプレス機
プレス機の倍力機構
図6 簡易概略図
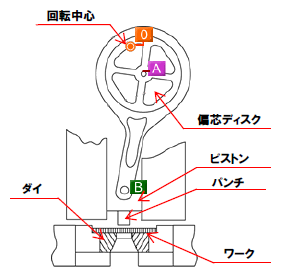
図7 ベクトル図
図6の機構は、クランクOAは偏芯ディスクを用いることで回転中心Oよりも下にディスク中心(=重心)が来たときに、
ディスク重量がワークをプレスするようになっているプレス機です。
中には、クランクとトグル機構が使われています。
図7はこの機構のベクトル図で、節Aと加工点Bにおける力のベクトル比較により、倍力作用が得られることが分かります。
つまり、偏芯ディスクを用いることでF0を大きくさせ、それをピストンにより垂直方向に変向してプレス力Fpを得ている機構です。
地球をてこで動かせるためには、どれぐらいの長さのてこが必要か?

「私に支点を与えよ。そうすれば地球をも動かして見せよう。」アルキメデスが残した有名な言葉です。
果たして、地球はてこで動かせるのでしょうか。動かせるとしたら、どれぐらの長さのてこが必要でしょうか。計算してみました。
地球の質量は5.9736 × 1024 kg, 約 6 × 1024 で、アルキメデスの体重を50kg、支点から作用点までを1kmと仮定すると、
力点でのモーメントと作用点でのモーメントが釣り合っているとして、支点から力点までの距離 d が求められます。
支点から力点までの距離
| 50kg | × | d | = | 6×1024kg | × | 1km |
| アルキメデスの体重(力点に加える力) | 支点から力点までの距離 | 地球の質量 | 支点から作用点までの距離 1km |
| d | = | 6×1024 kg × 1km | = | 1.2 × 1023 km |
| 50kg |
支点から力点までの距離が 1.2 × 1023 km、支点から作用点までの距離を1kmとすると、
必要なてこの長さは、120,000,000,000,000,000,000,001kmとなります。
1,000km/hのスピードで飛ぶ飛行機で移動すると約120,000,000,000,000,000,001時間がかかります。
人が100年まで生きると仮定した場合でも、136,986,301,000,000時間、 約136兆時間を飛ばないと着かない距離になってしまいます。
人の寿命が劇的に延びない限り、不可能な話ですね。