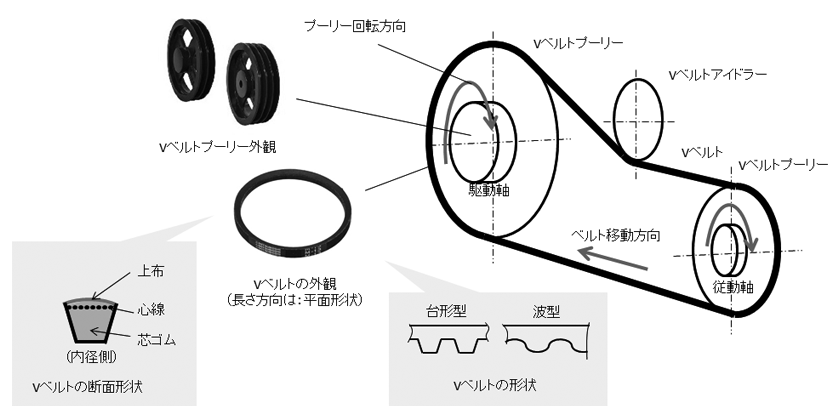
Vベルトとは、回転動力の伝達に用いられ、2本の回転軸にそれぞれVベルトプーリーを取り付けて、両軸をVベルトでつなぎ、その際発生する張力にVベルトアイドラーが必要回転運動を軸間で伝える機械要素部品である。
構造・用途・使用事例
構造
図1に示す様にその外観が円形状のVベルトを用いて、2個のVベルトプーリーをつなぎ、Vベルトアイドラーにて、Vベルトにテンションを加え、動力を伝える。
図1.Vベルトの構造
種類と特徴
回転力を伝える機械要素は表1に示す様な各種のものがあるが、Vベルトは、高速回転数、芯間距離大、低コストに特徴がある。
Vベルトによる動力の伝動は、Vベルトが、Vベルトプーリーの溝に食い込むことで、そのテンションが増大し、細いベルト形状で、動力を伝えることが出来る。
表1.回転力を伝える機械要素の種類と特徴
| Vベルト | タイミングベルト | チェーン | 平ベルト | 歯車 | |
|---|---|---|---|---|---|
| 構造 |  |
 |
 |
 |
 |
| 角度伝達 | 不可 | 可能(中精度) | 可能(低精度) | 不可 | 可能(高精度) |
| 動力伝達 | 中トルク | 中トルク | 大トルク | 低トルク | 大トルク |
| 回転数(音) | 高速(低) | 中速(大) | 低速(大) | 高速(低) | 高速(大) |
| 潤滑 | 不要 | 不要 | 必要 | 不要 | 必要 |
| 芯間距離 | 大 | 大 | 大 | 大 | 小 |
| サイズ | 大形 | 中形 | 小形 | 大形 | 小形 |
| コスト | 低 | 中 | 低 | 低 | 高価 |
使用事例
Vベルトを用いた回転動力の伝達事例を図2に示す。
図2.Vベルトによる従動軸の駆動事例
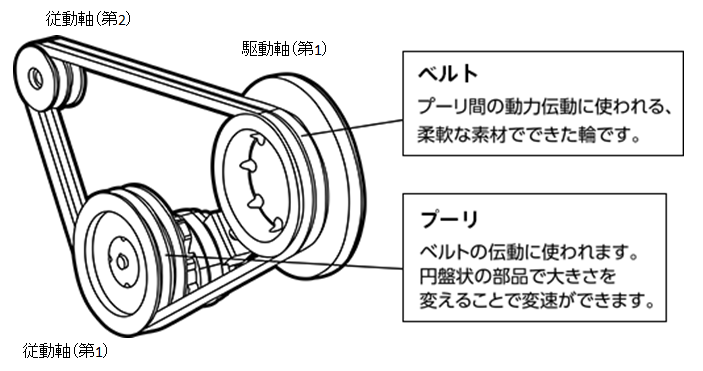
2本のベルトを使用し駆動軸で、2本の従動軸を駆動している。この図にはベルトのテンションを調整するVベルトアイドラーを使用していないが、従動軸(第2)の取り付け位置を変えることでそのテンションを調整可能としている。これらの商品は主に車両や回転機(モーター)などで使用されることが多い。
選定ポイント
選定ポイントは下記3点となる。
伝達動力、位置形状などに合わせたVベルトの選定
Vベルトの選定は選択項目の仕様を決めることが重要である。下表2に選定項目と選定ポイントを示す。
表2.Vベルトの選定項目とポイント
| 選定項目 | 選択のポイント | |
|---|---|---|
| 形状 | 寿命 |
|
| 断面 | 動力 |
|
| 使用本数 | 動力 |
|
| 長さ | 距離 |
|
| 強度 | 動力 |
|
| 材質 | 環境 |
|
| 速度 | 使用 |
|
Vベルトプーリーの選定
Vベルトプーリーは、Vベルトの寿命を決めるために重要な部品になる。またVベルトによる動力を伝導する際、ベルト長さ、速比などのキーポイントとなる。下表に選定項目と選定ポイントを示す。
表3.Vベルトプーリーの選定項目とポイント
| 選定項目 | 選択のポイント | |
|---|---|---|
| Vベルトプーリー径 | ベルト長さ |
|
| 速比 |
|
|
| 最小直径 |
|
|
| 動力 |
|
|
Vベルトアイドラーの選定と取り付け法
Vベルトによる動力伝達はVベルトの張力が必要で、その張力発生にVベルトアイドラーが必要となる。
動力伝達部品および使用箇所により、アイドラーの仕様が異なってくる。下表にその選定のポイントを示す。
表4.Vベルトアイドラーの選定項目とポイント
| 選定項目 | 選択のポイント | |
|---|---|---|
| アイドラー | 外形形状 |
|
| テンション調整構造 |
|
|
| 取付位置 |
|
|
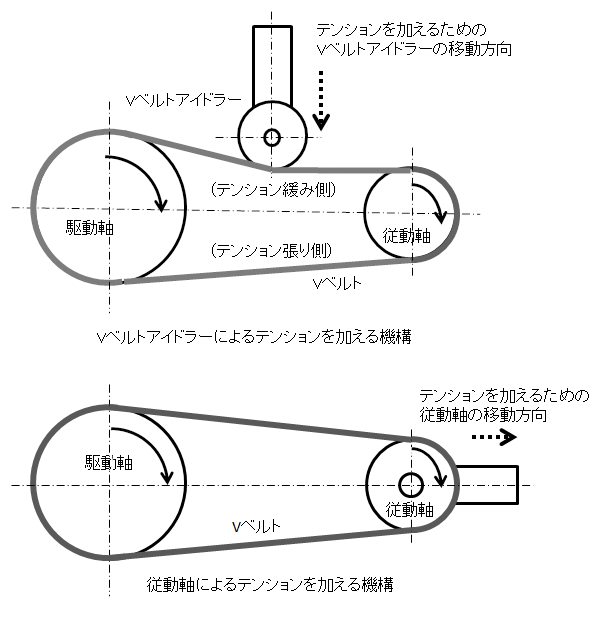
図3.Vベルトアイドラーのテンション調整構造図
回転動力の伝達
Vベルトによる動力の伝達はテンションの移動によって行われる。これはVベルトが駆動プーリーに巻き付く場合のその接点に発生するテンションで説明できる。図4を用いてこの動力伝達について説明する。
図4.Vベルト伝動による動力の伝達とベルトテンション
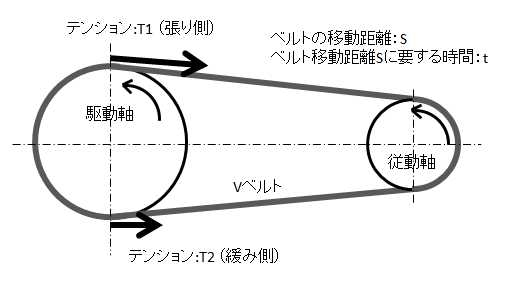
仕事は、力に移動距離を掛けた数字で表され、回転動力は仕事を力が移動に要した時間(t)で除した数字で表される。
従って、張り側のテンションであるT1による動力は、T1 × s/t、緩み側のテンションであるT2による動力の-T2 × s/tで示される。この符号が逆となるのは、ベルト上でそのテンションの向きが反対となるためである。従って伝達動力は、(T1-T2) × s/tとなる。
Vベルトを用いた動力伝達は、次の2点が必要となる
- ①
- Vベルトに張力が発生すること
- ②
- 駆動Vベルトプーリーの両端に加わる張力が異なること
従って、動力伝達のVベルトにテンションが必要となる。
ベルトのテンション
動力伝達するベルトのキーポイントとなるのは、テンションである。このテンションについて、力学計算*1 方法をまとめたものを下記に記載する。計算方法を簡略化するために、平ベルトのみを計算対象としている。
図4で示したように動力を伝達するためのトルクは、張り側のテンションから緩み側のテンションを差し引いた数字を用いたわけであるが、参照した資料に従って、両テンションを次の記号であらわすこととする。
- Te
- :有効テンション
- Tt
- :張り側テンション
- Ts
- :緩み側テンション
Te=Tt-Ts-------①
続いて、Vベルトプーリーに巻き付いたベルトの張力についてその力の釣り合いを評価する。この力の釣り合いは、次の点を仮定する。
- ベルトプーリーとベルトの摩擦力は一定である。
- ベルトプーリーと接するベルトのテンションは張り側に向かって徐々に増加する。
図5にベルトとベルトプーリーの力の釣り合いを示すモデル図を示す。
図5.平ベルトとプーリーの力の釣り合いモデル図
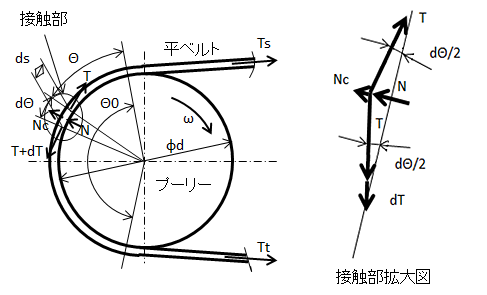
- Ts
- :有効テンション
- Tt
- :張り側テンション
- Te
- :緩み側テンション
- T
- :緩み側テンション
- T+dT
- :ベルト上張り側張力
- Θ
- :ベルト上の角度
- Θ0
- :ベルト上の巻き付け角度
- dΘ
- :ベルト上の微小角
- ω
- :プーリー回転角速度
- d
- :プーリー直径
- Nc
- :プーリーからの反力
ベルトの遠心力による半径方向に生ずる外向きの力は
Nc=m × ds × (d/s) × ω2=2 × m × v2 × ds/d=mv2dΘ--------②
従って、半径方向の力の釣り合いは
N=2T × sin(dΘ/2)+dT × sin(dΘ/2)-mv2 × dΘ-------③
ここで、dΘは微小であるから、sin(dΘ/2)=dΘ/2なので
dT × sin(dΘ/2)=0なので、③式は
N=(T-m × v2)dΘ--------④
円周方向の力の釣り合いは、摩擦力を考慮して、
T × cos(dΘ/2)+F=(T+dT) × cos(dΘ/2)--------⑤
摩擦力Fは、ベルトとベルトプーリーの摩擦力をµとすると、F=µNで与えられ、dΘは微小であるので、cos(dΘ/2)=1となる。従って、⑤式は
µN=dT---------⑥
となり、この式を④に代入して
µdΘ=dT/(T-mv2)--------⑦
⑦式を接触角Θについて積分すれば、
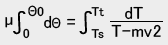
これから
(Tt-mv2)/(Ts-mv2)=eµΘ0--------⑧
となる。この式は、オイラーの式と呼ばれ、ベルトの伝動の基礎式として使われている。⑧式は
Ts=(Tt-mv2)e-µΘ0+mv2--------⑨
と変形出来て、①式に⑨式を代入すると、有効張力Teは、
Te=(Tt-mv2)(eµΘ0-1)/eµΘ0)---------⑩
この式から、有効張力Teは、摩擦係数µ、接触角Θ0、並びにベルトの遠心力mv2の影響を受けることが判る。ベルトの速度が増し、遠心力が張りテンションに一致すれば、有効張力は、ゼロになる。従って、この場合は、動力が伝達できなくなるので、ベルトを用いた動力の伝動において、ベルトの速度の制限が存在することになる。
注釈
- *1
- 日本機械学会「機械要素設計(JSMEテキストシリーズ):P127 ベルトの張力」より引用
おすすめ商品
Vベルト
Vベルトを規格やブランドから選ぶ
| ベルト形から探す | M A B C D 3V 5V 8V AX CX BX MB K LA/LB/LC AG-XB AG-XC 3M 5M 7M 11M |
|---|---|
| 列から探す | 1 2 3 |
| 特性から探す | 標準 高伝動 耐屈曲 耐熱 耐油 静電防止 耐摩耗 |
| ブランドから探す | 三ツ星ベルト バンドー化学 エスコ DONGIL RUBBER BELT |