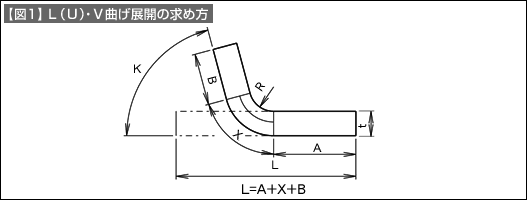
【図1】に示すような形状の曲げ展開をするには、直線部分(図にA、Bで示した部分)と曲げ部分(Xで示した部分)に分けて計算します。直線部分は変化が無いのでそのままの数値を使います。曲げ部分について計算して、直線部分と合計して、展開長さ(L=A+X+B)を求めます。
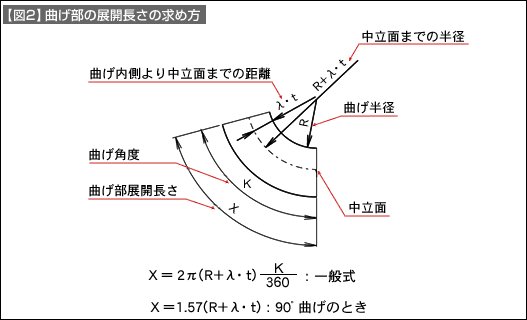
X部分は、曲げた内側の周長と外側の周長では長さが違います。元の長さより、外側は伸び、内側は短くなっています。しかし、板厚のどこかに変化しない長さ部分があります。この位置を中立面といいます。この位置を求め、弧の長さを求めることで曲げ展開長を知ることができます。
【図2】を参照に、曲げ部の展開長の求め方を説明します。まず、中立面の位置を求めます。中立面位置は、曲げ半径(R)と材料の板厚(t)との関係で変化します。また、曲げ法式(V曲げとL・U曲げ)の違いでも変化します(展開計算に入る前に曲げ法式は決めておく)。中立面までの距離はλ(ラムダ)という係数で表されます。その求め方は【表1】によります。λと板厚(t)の関係から中立面までの距離が分かり、中立面までの半径を知ることができます。周長を求める公式と曲げ角度から、弧の長さとして展開長を求めます(図2に、X=で示した式)。
【表1】λを求める表
|
|