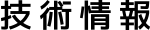
カール曲げ形状は【図1】のようになります。展開計算では、3/4円を形成する部分(L1)と、残り部分(L2)に分けて計算して、L=L1+L2として展開長さを求めます。
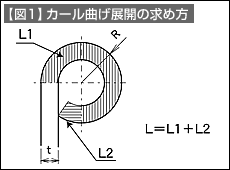
L1部分の展開長さの求め方を【図2】で説明します。まず、中立面までの距離を求めます。中立面までの係数(y)を、カール半径(R)と材料板厚(t)から【表1】を使って求めます。係数(y)が求められたら、カール半径(R)と係数(y)、および板厚(t)から中立面半径(r)を求め、中立面半径(r)の3/4円の周長を求めます。(【図2】でL1=の式)中立面半径(r)の3/4円の周長を求めます(図2でL1=の式)。
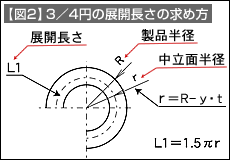
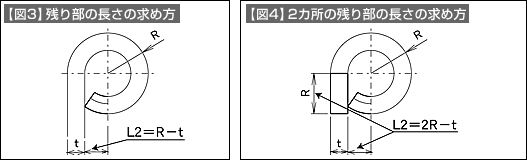
次に、残り部分の長さ(L2)を求めます。【図3】に示した内容です。この部分は円弧とせず直線として、カール半径(R)から材料板厚を引いた寸法と簡易な形で求めます。円弧として求めたときとの差が小さいからです。この部分の計算で、2R-tとしている式があります。これは曲げのない直線部分まで含めた計算(【図4】参照)をしているものです。どちらの計算方法をとってもかまいません。基準位置が変わりますから、その点に注意が必要です。
【表1】yを求める表
|