射出成形加工では、溶けたプラスチック(流体)がスプルーやランナーを通過して、キャビティの中に充填されます。
この現象を模式的に考えまてみますと、粘り気のある流体が、管の中を流れていくということに表現されます。
粘り気のある流体が、ある断面積の管の中を流れていく場合には、「流量の式」という基本的な状態を表現する計算式があります。
【流量の式】
Q=av
Q:流量(m3/sec)
a:流路の断面積(m2)
v:流体の流速(m/sec)
一定時間に管の中を流れる流体の体積Qは、流路(管)の断面積と流体の流速をかけることにより求めることができます。
流量を増加させるためには、流路の断面積aを大きくするか、流体の流速を早くすることが必要であることが式より分かります。
また、流量が一定である場合には、下記の式が成り立ちます。
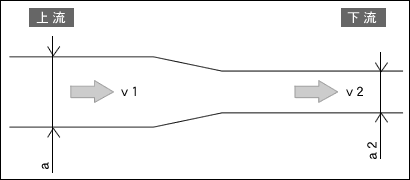
a1・v1=a2・v2
a1:上流の流路の断面積
a2:下流流路の断面積
v1:上流の流速
v2:下流の流速
つまり、流量が一定である場合には、流路の断面積が太い場合には、ゆっくりと流れますが、流路の断面積が細い場合には流速が早くなるということになります。
したがいまして、細いランナー内部やゲートを溶融プラスチックが流れる場合には流速が早くなるということになります。
ただし、溶融プラスチックの粘り気(粘性)は、時間経過によって変化しますので、厳密には上記式は、各種のファクターによって修正しなければなりません。