GPS:Geometrical Product Specifications
幾何特性に用いる記号と付加記号
幾何特性に用いる記号
| 公差の種類 | 特性 | 記号 | データム指示 | 参照 |
|---|---|---|---|---|
| 形状公差 | 真直度 |  |
否 | 18.1 |
| 平面度 |  |
否 | 18.2 | |
| 真円度 |  |
否 | 18.3 | |
| 円筒度 |  |
否 | 18.4 | |
| 線の輪郭度 |  |
否 | 18.5 | |
| 面の輪郭度 | 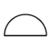 |
否 | 18.7 | |
| 姿勢公差 | 平行度 |  |
要 | 18.9 |
| 直角度 |  |
要 | 18.10 | |
| 傾斜度 | 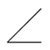 |
要 | 18.11 | |
| 線の輪郭度 |  |
要 | 18.6 | |
| 面の輪郭度 |  |
要 | 18.8 | |
| 位置公差 | 位置度 |  |
要・否 | 18.12 |
| 同心度(中心点に対して) |  |
要 | 18.13 | |
| 同軸度(軸線に対して) |  |
要 | 18.13 | |
| 対称度 | 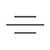 |
要 | 18.14 | |
| 線の輪郭度 |  |
要 | 18.6 | |
| 面の輪郭度 |  |
要 | 18.8 | |
| 振れ公差 | 円周振れ |  |
要 | 18.15 |
| 全振れ |  |
要 | 18.16 |
付加記号
| 説明 | 記号 | 参照 |
|---|---|---|
| 公差付き形体指示 | 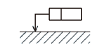 |
|
| データム指示 | 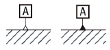 |
JIS B 0022 |
| データムターゲット | 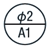 |
JIS B 0022 |
| 理論的に正確な寸法 |  |
|
| 突出公差域 |  |
ISO 10578 |
| 最大実体公差方式 |  |
JIS B 0023 |
| 最小実体公差方式 |  |
JIS B 0023 |
| 自由状態(非剛性部品) |  |
JIS B 0026 |
| 全周(輪郭度) | 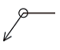 |
|
| 包絡の条件 |  |
JIS B 0024 |
| 共通公差域 |  |
幾何公差の定義
※「18.1」など冒頭の数値はJIS B 0021の項目番号を表します。
単位 mm
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.1 真直度公差 | ||
|
対象とする平面内で、公差域はtだけ離れ、指定した方向に、平行二直線によって規制される。
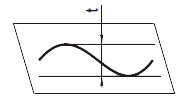 公差域はtだけ離れた平行二平面によって規制される。
備考 この意味は、旧 JIS B 0021とは異なる。  公差値の前に記号φを付記すると、公差域は直径tの円筒によって規制される。
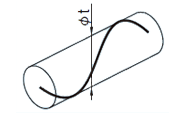 |
上側表面上で、指示された方向における投影面に平行な任意の実際の(再現した)線は、0.1だけ離れた平行二直線の間になければならない。
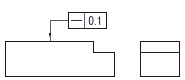 円筒表面上の任意の実際の(再現した)母線は、0.1だけ離れた平行二平面の間になければならない。
備考 母線についての定義は、標準化されていない。 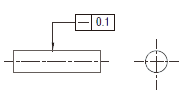 公差を適用する円筒の実際の(再現した)軸線は、直径0.08の円筒公差域の中になければならない。
 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.2 平面度公差 | ||
|
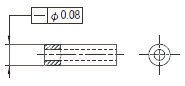
公差域は、距離tだけ離れた平行二平面によって規制される。
 |
実際の(再現した)表面は、0.08だけ離れた平行二平面の間になければならない。
 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.3 真円度公差 | ||
|
対象とする横断面において、公差域は同軸の二つの円によって規制される。
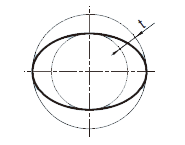 |
円筒及び円すい表面の任意の横断面において、実際の(再現した)半径方向の線は半径距離で0.03だけ離れた共通平面上の同軸の二つ円の間になければならない。
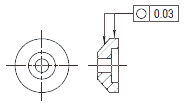 円すい表面の任意の横断面内において、実際の(再現した)半径方向の線は半径距離で0.1だけ離れた共通平面上の同軸の二つの円の間になければならない。
備考 半径方向の線に対する定義は、標準化されていない。 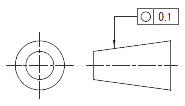 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.4 円筒度公差 | ||
|
公差域は、距離tだけ離れた同軸の二つの円筒によって規制される。
 |
実際の(再現した)円筒表面は、半径距離で0.1だけ離れた同軸の二つの円筒の間になければならない。
 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.5 データムに関連しない線の輪郭度公差 (ISO 1660) | ||
|
公差域は、直径tの各円の二つの包絡線によって規制され、それらの円の中心は理論的に正確な幾何学形状をもつ線上に位置する。
 |
指示された方向における投影面に平行な各断面において、実際の(再現した)輪郭線は直径 0.04の、そしてそれらの円の中心は理想的な幾何学形状をもつ線上に位置する円の二つの包絡線の間になければならない。
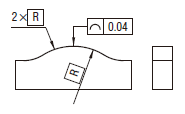 |
|
| 18.6 データムに関連した線の輪郭度公差 (ISO 1660) | ||
|
公差域は、直径tの各円の二つの包絡線によって規制され、それらの円の中心はデータム平面A及びデータム平面Bに関して理論的に正確な幾何学形状をもつ線上に位置する。
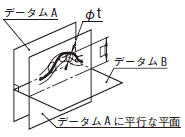 |
指示された方向における投影面に平行な各断面において、実際の(再現した)輪郭線は直径 0.2の、そしてそれらの円の中心はデータム平面A及びデータム平面Bに関して理論的な幾何学輪郭をもつ線上に位置する円の二つの包絡線の間になければならない。
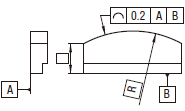 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.7 データムに関連しない面の輪郭度公差 (ISO 1660) | ||
|
公差域は、直径tの各球の二つの包絡線によって規制され、それらの球の中心は理論的に正確な幾何学形状をもつ線上に位置する。
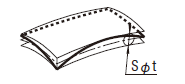 |
実際の(再現した)表面は、直径0.02の、それらの球の中心が理論的に正確な幾何学形状をもつ表面上に位置する各球の二つの包絡面の間になければならない。
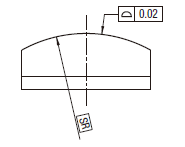 |
|
| 18.8 データムに関連した面の輪郭度公差 (ISO 1660) | ||
|
公差域は、直径tの各球の二つの包絡面によって規制され、それらの球の中心はデータム平面Aに関して理論的に正確な幾何学形状をもつ表面上に位置する。
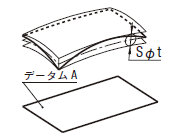 |
実際の(再現した)表面は、直径0.1の、それらの球の二つの等間隔の包絡面の間にあり、その球の中心はデータム平面 Aに関して理論的な幾何学形状をもつ表面上に位置する。
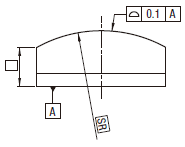 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.9 平行度公差 | ||
| 18.9.1 データム直線に関連した線の平行度公差 | ||
|
公差域は、距離tだけ離れた平行二平面によって規制される。それらの平面は、データムに平行で、指示された方向にある。
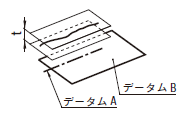 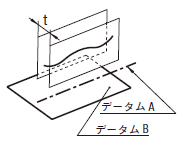 公差域は、距離t1及びt2だけ離れ、互いに直角な平行二平面によって規制され、それらの平面はデータム軸直線に平行で、指示された方向にある。
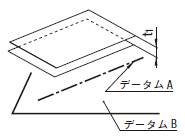  もし、公差値の前に記号φが付記されると、公差域はデータムに平行な直径tの円筒によって規制される。
 |
実際の(再現した)軸線は、0.1だけ離れ、データム軸直線Aに平行で、指示された方向にある平行二平面の間になければならない。
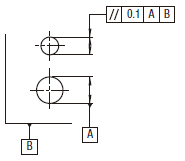 実際の(再現した)軸線は、0.1だけ離れ、データム軸直線 A(データム軸線)に平行で、指示された方向にある平行二平面の間になければならない。
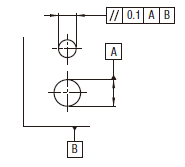 実際の(再現した)軸線は、それぞれ指示された方向に互いに直角な平行二平面が0.2及び0.1だけ離れた間になければならない。平行二平面は、データム軸直線Aに平行でなければならない。
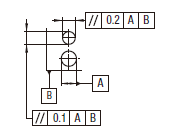 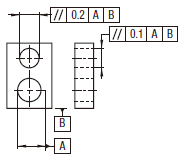 実際の(再現した)軸線は、データム軸直線Aに平行な直径0.03の円筒公差域の中になければならない。
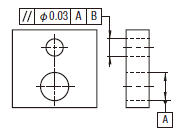 |
|
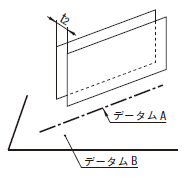
| 18.9.2 データム平面に関連した線の平行度公差 | ||
|
公差域は、距離tだけ離れ、データム平面Bに平行な平行二平面によって規制される。
 |
実際の(再現した)軸線は、0.01だけ離れ、データム平面Bに平行な平行二平面の間になければならない。
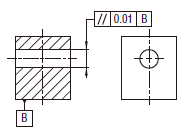 |
|
| 18.9.3 データム直線に関連した表面の平行度公差 | ||
|
公差域は、距離tだけ離れ、データム軸直線に平行な平行二平面によって規制される。
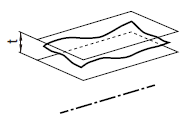 |
実際の(再現した)表面は、0.1だけ離れ、データム軸直線Cに平行な平行二平面の間になければならない。
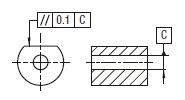 |
|
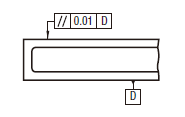
| 18.9.4 データム平面に関連した表面の平行度公差 | ||
|
公差域は、距離tだけ離れ、データム平面に平行な平行二平面によって規制される。
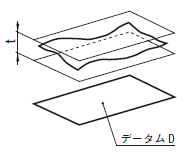 |
実際の(再現した)表面は、0.01だけ離れ、データム平面Dに平行な平行二平面の間になければならない。
 |
|
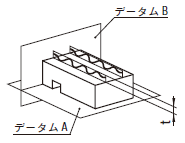
| 18.9.5 データム平面に関連した線要素の平行度公差 | ||
|
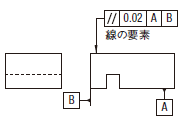
公差域は、距離tだけ離れ、データム平面Aに平行で、データム平面Bに直角な平行二直線によって制限される。
 |
実際の(再現した)表面は、0.02だけ離れ、データム平面Aに平行で,データム平面Bに直角な平行二直線の間になければならない。
 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.10 直角度公差 | ||
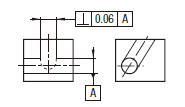
| 18.10.1 データム軸直線に関連した線の直角度公差 | ||
|
公差域は、距離tだけ離れ、データムに直角な平行二平面によって規制される。
 |
実際の(再現した)軸線は、0.06だけ離れ、データム軸直線Aに直角な平行二平面の間になければならない。
 |
|
| 18.10.2 データム平面に関連した線の直角度公差 | ||
|
公差域は、距離tだけ離れ、平行二平面によって規制される。この平面は、データムに直角である。
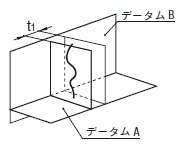
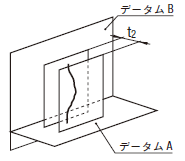
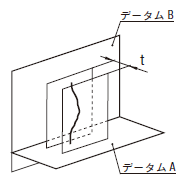 公差域は、距離t1及びt2だけ離れ、互いに直角な二対の平行二平面によって規制される。その平面は、データムに直角で、指示された方向にある。
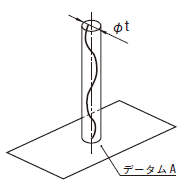
  公差値の前に記号φが付記されると、公差域はデータムに直角な直径tの円筒によって規制される。
 |
円筒の実際の(再現した)軸線は、0.1だけ離れ、データム平面Aに直角な平行二平面の間になければならない。
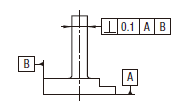 円筒の実際の(再現した)軸線は、0.1及び0.2だけ離れ、指示された方向で、互いに直角な二対の平行二平面の間になければならない。二対の平行二平面は、データム平面Aに直角でなければならない。
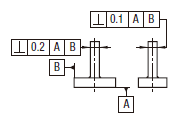 円筒の実際の(再現した)軸線は、データム平面Aに直角な直径0.1の円筒公差域の中になければならない。
 |
|
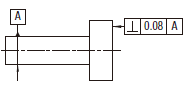
| 18.10.3 データム直線に関連した表面の直角度公差 | ||
|
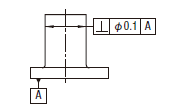
公差域は、距離tだけ離れ、データムに直角な平行二平面によって制限される。
 |
実際の(再現した)表面は、0.08だけ離れ、データム軸直線Aに直角な平行二平面の間になければならない。
 |
|
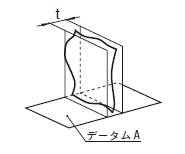
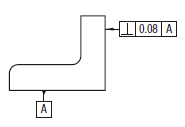
| 18.10.4 データム平面に関連した表面の直角度公差 | ||
|
公差域は、距離tだけ離れ、データムに直角な平行二平面によって規制される。
 |
実際の(再現した)表面は、0.08だけ離れ、データム平面Aに直角な平行二平面の間になければならない。
 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.11 傾斜度公差 | ||
| 18.11.1 データム直線に関連した直線の傾斜度公差 | ||
|
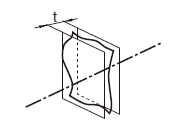
a) 同一平面内における線及びデータム直線公差域は、距離tだけ離れ、データム直線に対して指定された角度で傾斜した平行二平面によって制限される。
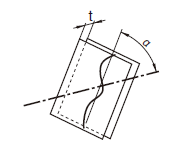 b) 異なった平面内における線及びデータム直線公差域は、tだけ離れ、データムに対して指示した角度で傾斜した平行二平面によって規制される。もし、対象とした線及びデータムが同じ平面内にない場合には、公差域はデータムを含み、対象とした線に平行な平面上に対象とした線を投影して適用する。
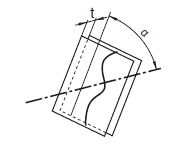 |
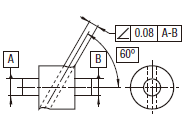
実際の(再現した)軸線は、データム軸直線 A-Bに対して理論的に正確に60°傾き、0.08だけ離れた平行二平面の間になければならなない。
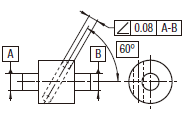
 データム軸直線を含む一平面上に投影した実際の(再現した)軸線は、共通データム軸直線A-Bに対して理論的に正確に60°傾斜し、0.08だけ離れた平行二平面の中になければならない。
 |
|
| 18.11.2 データム平面に関連した直線の傾斜度公差 | ||
|
公差域は、距離tだけ離れ、データムに対して指定された角度で傾いた平行二平面によって規制される。
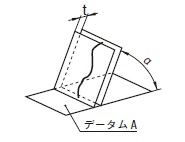 公差値に記号φが付いた場合には、公差域は直径tの円筒によって規制される。円筒公差域は、一つのデータムに平行で、データムAに対して指定された角度で傾いている。
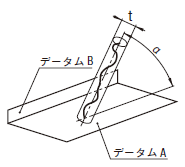 |
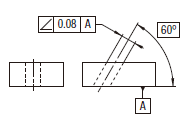
実際の(再現した)軸線は、互いに直角なデータムA及びデータムBに直角で、データム平面Aに対して理論的に正確に60°傾き、0.08だけ離れた平行二平面の間になければならない。
 実際の(再現した)軸線は、データムBに対して平行で、データム平面Aに対して理論的に正確に60°傾いた直径0.1の円筒公差域の中になければならない。
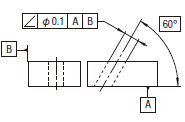 |
|
| 18.11.3 データム直線に関連した平面の傾斜度公差 | ||
|
公差域は、距離tだけ離れ、データムに対して指定した角度で傾斜した平行二平面によって規制される。
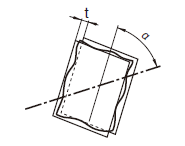 |
実際の(再現した)表面は、0.1だけ離れ、データム軸直線Aに対して理論的に正確に75°傾いた平行二平面の間になければならない。
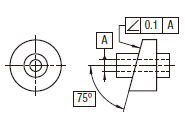 |
|
| 18.11.4 データム平面に関連した平面の傾斜度公差 | ||
|
公差域は、距離tだけ離れ、データムに対して指定した角度で傾いた平行二平面によって規制される。
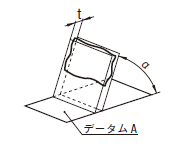 |
実際の(再現した)表面は、0.08だけ離れ、データム平面Aに対して理論的に正確に40°傾斜した平行二平面の間になければならない。
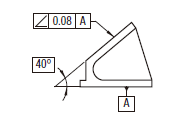 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.12 位置度公差 | ||
| 18.12.1 点の位置度公差 | ||
|
公差値に記号Sφが付いた場合には、その公差域は直径tの球によって規制される。球形公差域の中心は、データムA、B及びCに関して理論的に正確な寸法によって位置付けられる。
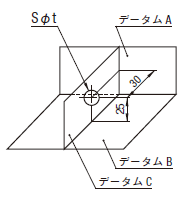 |
球の実際の(再現した)中心は、直径0.3の球形公差域の中になければならない。その球の中心は、データム平面A、B及びCに関して球の理論的に正確な位置に一致しなければならない。
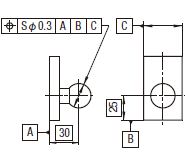 |
|
| 18.12.2 線の位置度公差 | ||
|
公差域は、距離tだけ離れ、中心線に対称な平行二直線によって規制される。その中心線は、データムAに関して理論的に正確な寸法によって位置付けられる。公差は、一方向にだけ指示する。
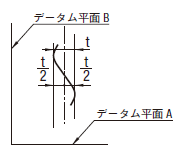 公差域は、それぞれ距離t1及びt2だけ離れ、その軸線に関して対称な2対の平行二平面によって規制される。その軸線は、それぞれデータムA、B及びCに関して理論的に正確な寸法によって位置付けられる。公差は、データムに関して互いに直角な二方向で指示される。
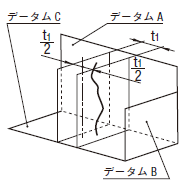 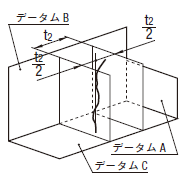 公差値に記号φが付けられた場合には、公差域は直径tの円筒によって規制される。その軸線は、データムC、A及びBに関して理論的に正確な寸法によって位置付けられる。
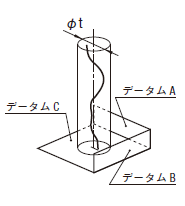 |
それぞれの実際の(再現した)けがき線は、0.1だけ離れ、データム平面A及びBに関して対象とした線の理論的に正確な位置について対称に置かれた平行二直線の間になければならない。
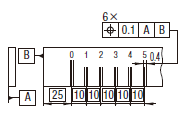 個々の穴の実際の(再現した)軸線は、水平方向に0.05、垂直方向に0.2だけ離れ、すなわち、指示した方向で、それぞれ直角な個々の2対の平行二平面の間になければならない。平行二平面の各対は、データム系に関して正しい位置に置かれ、データム平面C、A及びBに関して対象とする穴の理論的に正確な位置に対して対称に置かれる。
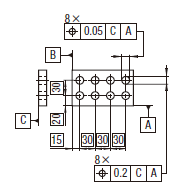 実際の(再現した)軸線は、その穴の軸線がデータム平面C、A及びBに関して理論的に正確な位置にある直径0.08の円筒公差域の中になければならない。
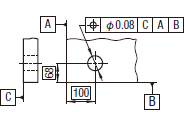 個々の穴の実際の(再現した)軸線は、データム平面A、B及びCに関して理論的に正確な位置にある0.1の円筒公差域の中になければならない。
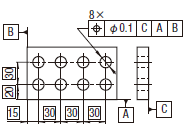 |
|
| 18.12.3 平たん(坦)な表面又は中心平面の位置度公差 | ||
|
公差域は、tだけ離れ、データムA及びデータムBに関して理論的に正確な寸法によって位置付けられた理論的に正確な位置に対称に置かれた平行二平面によって規制される。
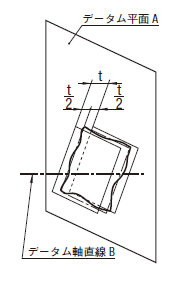 |
実際の(再現した)表面は、0.05だけ離れ、データム軸直線B及びデータム平面Aに関して表面の理論的に正確な位置に対して対称に置かれた平行二平面の間になければならない。
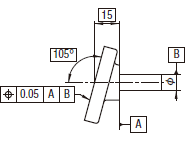 実際の(再現した)中心平面は、0.05だけ離れ、データム軸直線Aに対して中心平面の理論的に正確な位置に対して対称に置かれた平行二平面の間になければならない。
 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
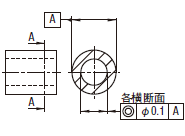
| 18.13 同心度公差及び同軸度公差 | ||
| 18.13.1 点の同心度公差 | ||
|
公差値に記号φが付けられた場合には、公差域は、直径tの円によって規制される。円形公差域の中心は、データム点Aに一致する。
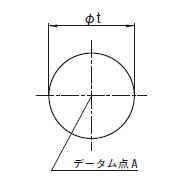 |
外側の円の実際の(再現した)中心は、データム円Aに同心の直径0.1の円の中になければならない。
 |
|
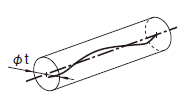
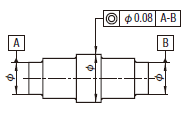
| 18.13.2 軸線の同軸度公差 | ||
|
公差値に記号φが付けられた場合には、公差域は直径tの円筒によって規制される。円筒公差域の軸線は、データムに一致する。
 |
内側の円筒の実際の(再現した)軸線は、共通データム軸直線A-Bに同軸の直径0.08の円筒公差域の中になければならない。
 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.14 対称度公差 | ||
| 18.14.1 中心平面の対称度公差 | ||
|
公差域は、tだけ離れ、データムに関して中心平面に対称な平行二平面によって規制される。
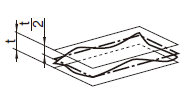 |
実際の(再現した)中心平面は、データム中心平面Aに対称な0.08だけ離れた平行二平面の間になければならない。
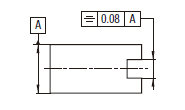 実際の(再現した)中心平面は、共通データム中心平面ABに対称で、0.08 だけ離れた平行二平面の間になければならない。
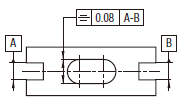 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
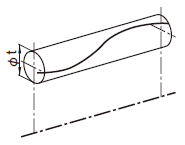
| 18.15 円周振れ公差 | ||
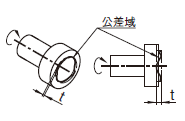
| 18.15.1 円周振れ公差-半径方向 | ||
|
公差域は、半径がtだけ離れ、データム軸直線に一致する同軸の二つの円の軸線に直角な任意の横断面内に規制される。
通常、振れは軸のまわりに完全回転に適用されるが、1回転の一部分に適用するために規制することができる。 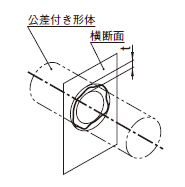 |
回転方向の実際の(再現した)円周振れは、データム軸直線Aのまわりを、そしてデータム平面Bに同時に接触させて回転する間に、任意の横断面において0.1以下でなければならない。
 実際の(再現した)円周振れは、共通データム軸直線A-Bのまわりに1回転させる間に、任意の横断面において0.1以下でなければならない。
 回転方向の実際の(再現した)円周振れは、データム軸直線Aのまわりに回転させる間公差を指示した部分を測定するときに、任意の横断面において0.2以下でなければならない。
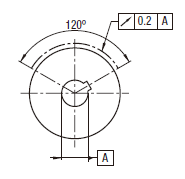  |
|
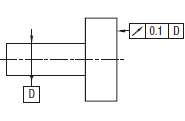
| 18.15.2 円周振れ公差-軸方向 | ||
|
公差域は、その軸線がデータムに一致する円筒断面内にあるtだけ離れた二つの円によって任意の半径方向の位置で規制される。
 |
データム軸直線Dに一致する円筒軸において、軸方向の実際の(再現した)線は0.1 離れた、二つの円の間になければならない。
 |
|
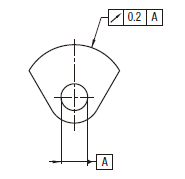
| 18.15.3 任意の方向における円周振れ公差 | ||
|
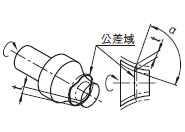
公差域は、tだけ離れ、その軸線がデータムに一致する任意の円すいの断面の二つの円の中に規制される。特に指示した場合を除いて、測定方向は表面の形状に垂直である。
 |
実際の(再現した)振れは、データム軸直線Cのまわりに1回転する間に、任意の円すいの断面内で 0.1以下でなければならない。
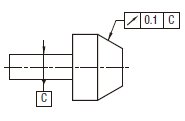 曲面の実際の(再現した)振れは、データム軸直線Cのまわりに1回転する間に、円すいの任意の断面内で0.1以下でなければならない。
 |
|
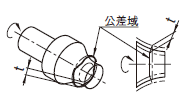
| 18.15.4 指定した方向における円周振れ公差 | ||
|
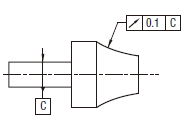
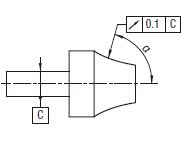
公差域は、tだけ離れ、その軸線がデータムに一致する二つの円によって、指定した角度の任意の測定円すい内で規制される。
 |
指定した方向における実際の(再現した)円周振れは、データム軸直線Cのまわりに1回転する間に、円すいの任意の断面内で0.1以下でなければならない。
 |
|
| 記号 | 公差域の定義 | 指示方法及び説明 |
|---|---|---|
| 18.16 全振れ公差 | ||
| 18.16.1 円周方向の全振れ公差 | ||
|
公差域は、tだけ離れ、その軸線はデータムに一致した二つの同軸円筒によって規制される。
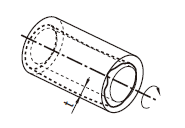 |
実際の(再現した)表面は、0.1の半径の差で、その軸線が共通データム軸直線A-Bに一致する同軸の二つの円筒の間になければならない。
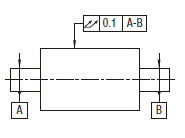 |
|
| 18.16.2 軸方向の全振れ公差 | ||
|
公差域は、tだけ離れ、データムに直角な平行二平面によって規制される。
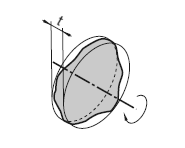 |
実際の(再現した)表面は、0.1だけ離れ、データム軸直線Dに直角な平行二平面の間になければならない。
 |
|