ボルト/ナットで締結した時の力のつりあい基礎（ねじ-11）

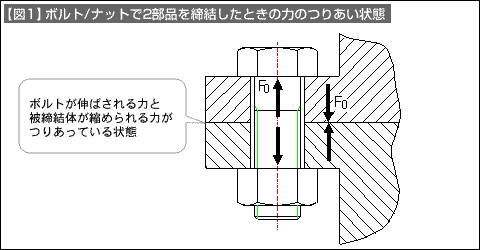
　ボルトとナットで2個の部品を締結した状態の力のつりあいで、締結状態の適正さ、締付けのゆるみ、ボルト破断などの判断が可能となります。ここでは基本的な解説をします。

（1）ボルト/ナットで締結した時の力のつりあい

（a）

ボルトとナットで2個の部品を締結した時、ボルト自体は引き伸ばす力（軸力）を受け、2個の被締結体は同じ力の圧縮力が作用します。この状態で、締結部は力のつりあいが取れます（【図1】）。

（b）

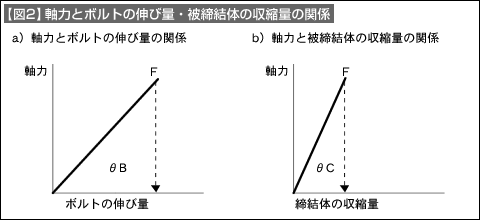
縦軸に軸力、横軸にボルトの伸び量・被締結体の縮み量をとったグラフでa）状態を示すと【図2】となります。

（c）

【図2】の2つの図の軸力は等しいので、これらのグラフを背中合わせに配置して合成グラフとしたのが【図3】で「締付け線図」と呼ばれます。

（d）

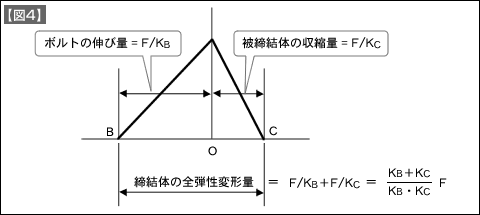
【図3】より、
tanθ_B ＝ 軸力÷ボルトの伸び量＝ F÷△_B ＝ ボルトのばね定数（K_B）
tanθ_C ＝ 軸力÷被締結体の伸び量＝ F÷△_C ＝ 被締結体のばね定数（K_C）
　したがって、
　　ボルトの伸び量△_B＝ F÷K_B ＝ F/ K_B・・・（1）
　　被締結体の伸び量△_C ＝ F÷K_C＝F/ K_C・・・（2）

（e）

【図3】を式（1）、（2）で表現すると【図4】となります。この場合、弾性変形の範囲での締結では【図4】の三角形FBCは常に相似となります。したがって、軸力と（ボルトと被締結体の合計の変形量）の比が常に一定となり、この比率を「へたり係数：Z」または｢締結体全体のばね定数｣と呼びます。

へたり係数：Z	＝	軸力÷ボルトと被締結体の合計の変形量
	＝	F÷F（KB＋KC）/ KB・KC ＝ KB・KC /（KB＋KC）

• « 前の講座へ
• 次の講座へ »